Multiple Linear Regression Code Example
이번 글에서는 Y를 결정하는 X의 요인이 하나가 아닌 여러개인 데이터에서 Y를 예측하는 다중선형회귀 코드에 대해서 알아보도록 하겠습니다.
이번에도 학습 환경은 Jupyter Notebook을 사용하였습니다.
필요한 라이브러리 import하기
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import hvplot.pandas
#jupyter notebook을 실행한 브라우저에서 바로 그림을 볼 수 있게 하는 코드입니다.
%matplotlib inline데이터를 읽어들입니다.
#데이터 경로의 경우 사용자의 환경에 맞게 설정해 주셔야 합니다.
df = pd.read_csv("C:/Users/User/Downloads/USA_Housing.csv")이번 데이터는 kaggle에서 가져온 미국 집값에 대한 예측입니다.(링크)
데이터가 어떤 변수들을 가지고 있는지 확인해봅시다.
df.head()
Adress 같은 경우는 변수들에게 영향을 미치지 않기 때문에 제거하도록 하겠습니다.
df = df.drop(['Address'], axis = 1)
각 변수들간의 상관관계를 알아보기
각 변수들이 서로에게 미치는 영향을 알아보기 위해 다음과 같은 코드를 사용합니다.
df.corr()

df.corr()를 통해 각각의 상관관계를 수치로 알 수 있습니다.
하지만 이렇게 수치로 보면 알아보기 어렵기 때문에 눈에 더 잘 들어올 수 있는 시각화를 해보도록 하겠습니다.
seaborn에서 제공하는 heatmap을 통해 각각변수들의 상관관계를 시각적으로 파악할 수 있습니다.
sns.heatmap(df.corr(), annot=True)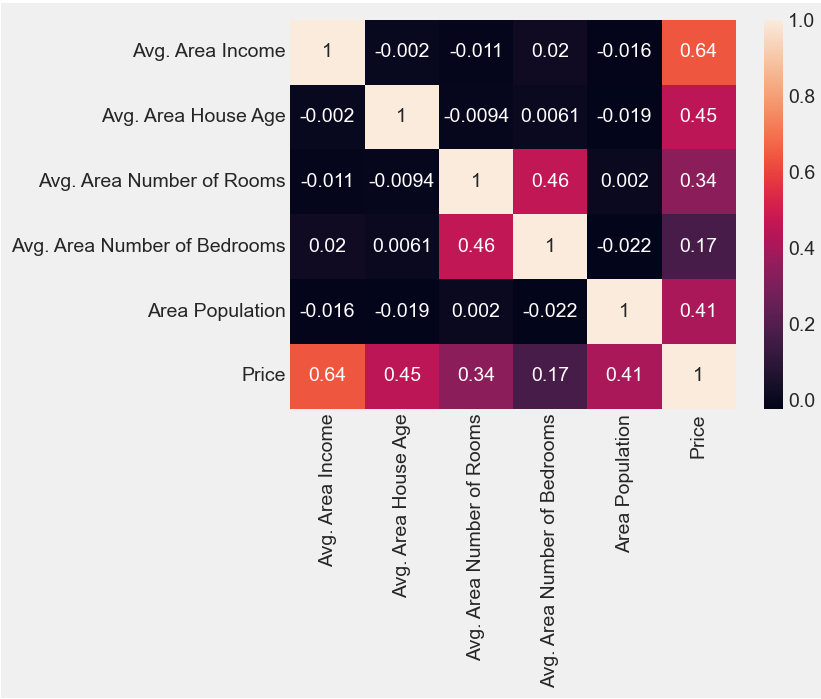
Price에 대한 나머지 변수들의 상관관계가 차례대로 0.64, 0.45, 0.34, 0.17, 0.41이 나왔습니다.
이 수치가 1에 가까울수록 서로가 양의 상관관계를 가지고 있고 하나의 값이 커질 때 다른 값이 커지는 경향성을 보인다고 할 수 있습니다.
반대로 이 수치가 -1에 가까울수록 서로가 음의 상관관계를 가지고 있고 하나의 값이 커질 때 다른 값이 작아지는 경향을 보인다고 할 수 있습니다.
모델 학습시키기
우리는 여러 변수들에 대한 집값의 상관관계를 파악해 집값을 예측하고자 합니다. 따라서 Price Column에 있는 데이터를 Y로 두고 나머지 변수들을 X로 두겠습니다.
x = df[['Avg. Area Income', 'Avg. Area House Age', 'Avg. Area Number of Rooms',
'Avg. Area Number of Bedrooms', 'Area Population']]
y = df['Price']지난번 단순회귀에서는 데이터를 나누지 않고 모든 데이터를 학습에 쓰고 임의의 값을 넣어 예측값을 나타내 보았습니다.
단순회귀에서는 크게 문제가 되지 않지만 많은 변수들을 학습해야하는 경우에는 모든 데이터를 학습데이터로 썼을 때, 학습에만 정확한 예측을 하고 새로운 데이터에 대한 예측은 성능이 좋지 못한 현상이 나타나는데, 이를 과적합(Overfitting)현상이라고 합니다.
이런 현상을 막기 위해 우리는 데이터를 train set과 test set으로 나누어서 학습을 진행하겠습니다.(Validation set도 존재하지만 여기서는 train, test로만 나누도록 하겠습니다.)
다음 코드를 통해 데이터를 나누어 보도록 하겠습니다.
from sklearn.model_selection import train_test_split
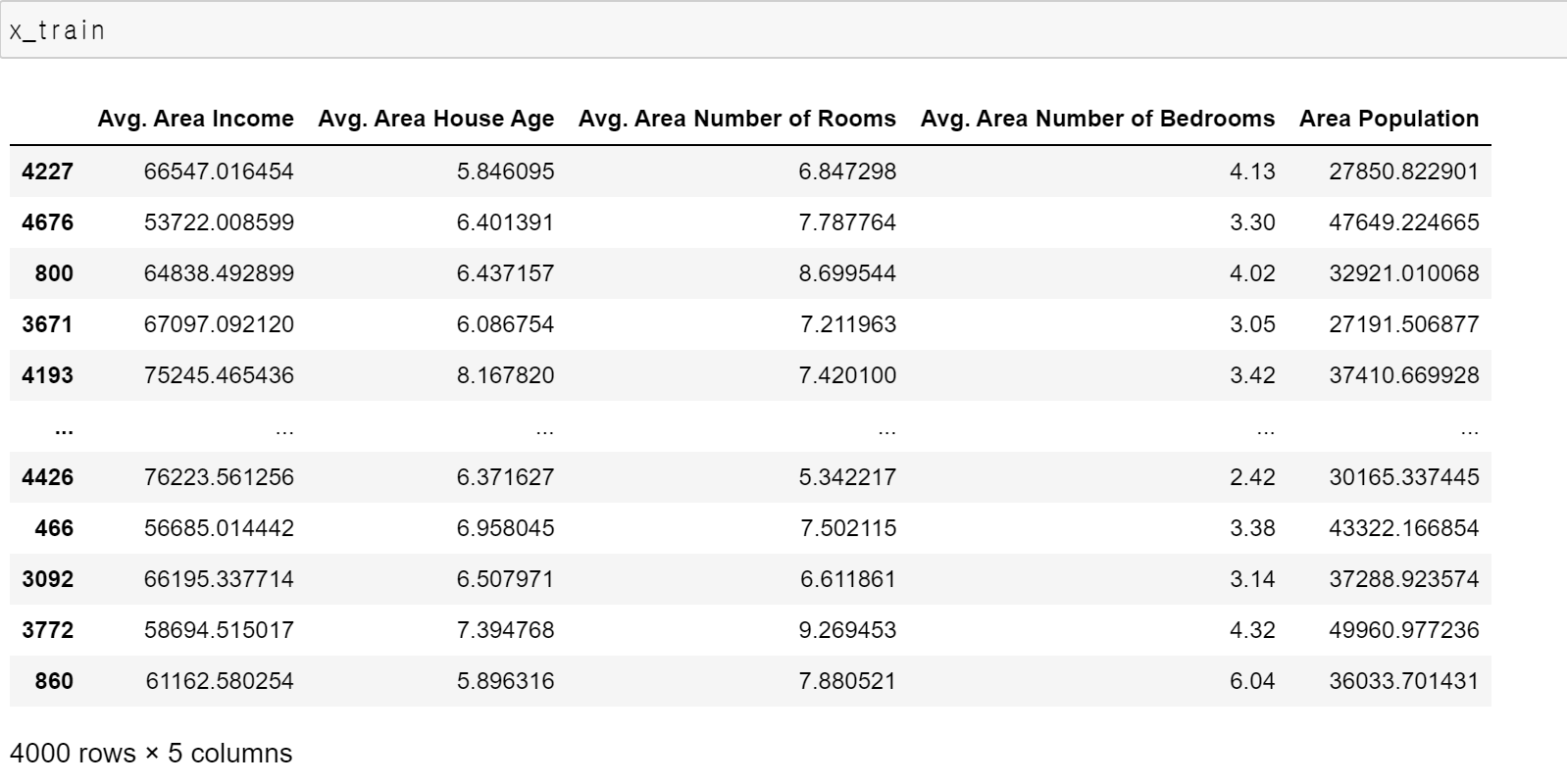
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2, random_state=42)x_train
x_train은 학습할 x 변수들의 데이터입니다.
x_test
x_test는 테스트를 위한 x 변수들의 데이터 입니다.
y_train
y_train은 학습에 사용할 x_train에 대한 y의 데이터입니다.

(원래 Price 데이터는 지수표현식으로 나왔지만 보기 편하게 하기위해 지수표현식을 없애서 나타내었습니다.)
y_test
y_test는 테스트에 사용할 x_test에 대한 y의 데이터입니다.
test_size = 0.2
test_size는 전체 데이터에서 test데이터가 차지하는 비율을 의미합니다.
따라서 전체 데이터의 0.2가 test데이터가되고 5000개의 데이터 중에 4000개의 데이터가 train data가 되고
나머지 1000개의 데이터가 test data가 됩니다.
random_state = 42
random_state는 각 학습마다 train, test 데이터를 어떤식으로 나누어서 설정할지에 대한 코드입니다. 만약 random_state를 설정하지 않으면 컴퓨터는 각 학습마다 다른 데이터를 train/test 데이터로 나누게 될 것입니다.
random_state를 정수로 고정하면 컴퓨터는 그 정수에 따라 일정한 패턴의 데이터를 train/test 데이터로 나누게 됩니다.
학습을 위한 함수들을 미리 정의
from sklearn import metrics
from sklearn.model_selection import cross_val_score
def cross_val(model):
pred = cross_val_score(model, x, y, cv=10)
return pred.mean()
def print_evaluate(true, predicted):
mae = metrics.mean_absolute_error(true, predicted)
mse = metrics.mean_squared_error(true, predicted)
rmse = np.sqrt(metrics.mean_squared_error(true, predicted))
r_square = metrics.r2_score(true, predicted)
print('MAE:', mae)
print('MSE:', mse)
print('RMSE:', rmse)
print('R_Square', r_square)
print('__________________________________')
def evaluate(true, predicted):
mae = metrics.mean_absolute_error(true, predicted)
mse = metrics.mean_squared_error(true, predicted)
rmse = np.sqrt(metrics.mean_squared_error(true, predicted))
r_square = metrics.r2_score(true, predicted)
return mae, mse, rmse, r_square학습을 위한 함수들을 미리 정의해 놓겠습니다.
각각 함수의 의미에 대해서는 밑에서 간단하게 설명하겠습니다.
sklearn.pipeline을 사용한 학습과정 단순화
sklearn이 제공하는 pipeline을 사용하면 데이터 전처리, 표준화등의 작업을 단순화 시킬 수 있습니다.
(추후 pipeline의 기능에 대해서 자세히 설명하겠습니다.)
from sklearn.preprocessing import StandardScaler
from sklearn.pipeline import Pipeline
pipeline = Pipeline([
('std_scalar', StandardScaler())
])
x_train = pipeline.fit_transform(x_train)
x_test = pipeline.transform(x_test)train 데이터를 이용해 Linear Regression학습
from sklearn.linear_model import LinearRegression
lin_reg = LinearRegression()
lin_reg.fit(x_train,y_train)x_train과 y_train을 사용해 linear regression학습을 진행하였습니다.
절편(bias)과 가중치(Weight) 확인하기
학습이 끝난 모델을 토대로 절편과 가중치 값들을 구해보겠습니다.
# 학습이 끝난 모델의 절편 구하기
print(lin_reg.intercept_)절편을 구해보면
1229576.9925600903이렇게 값이 나오게 됩니다.
다음은 가중치들을 구해보도록 하겠습니다.
우리가 사용한 데이터의 x 변수들이 여러개 있기 때문에 가중치도 그에 맞게 나올것입니다.
coeff_df = pd.DataFrame(lin_reg.coef_, x.columns, columns=['Coefficient'])
coeff_df
test 데이터로 학습한 모델을 확인하기
이제 학습의 마지막 단계가 남았습니다.
우리가 4000개의 train 데이터로 학습한 모델을 나머지 1000개의 test 데이터로 비교하여 얼마나 예측을 잘 했는지 알아보도록 하겠습니다.
pred = lin_reg.predict(x_test)
위의 코드를 통해 x_test에 대한 예측값들이 구해졌을 것입니다.
그럼 x_test에 대한 예측값들을 우리가 미리 split 해둔 y_test 값들과 비교해보도록 하겠습니다.
pd.DataFrame({'True Values': y_test, 'Predicted Values': pred}).hvplot.scatter(x='True Values', y='Predicted Values')
그림 7과 같이 실제값과 예측값의 데이터가 우상향 하는 것을 볼 수 있습니다.
다음은 실제값과 예측값의 차를 그래프로 나타내 보겠습니다.
pd.DataFrame({'Error Values': (y_test - pred)}).hvplot.kde()
그림 8.과 같이 실제 데이터 값과 우리가 학습을 통해 예측한 값의 차가 어느정도 정규분포를 따른다고 볼 수 있습니다.
마지막으로 각각의 데이터의 오차들을 다음과 같이 알아보겠습니다.
test_pred = lin_reg.predict(x_test)
train_pred = lin_reg.predict(x_train)
print('Test set evaluation:\n_____________________________________')
print_evaluate(y_test, test_pred)
print('Train set evaluation:\n_____________________________________')
print_evaluate(y_train, train_pred)
results_df = pd.DataFrame(data=[["Linear Regression", *evaluate(y_test, test_pred) , cross_val(LinearRegression())]],
columns=['Model', 'MAE', 'MSE', 'RMSE', 'R_Square', "Cross Validation"])
그림 9.를 살펴보겠습니다.
MAE는 Mean Absolute Error로 실제값과 예측값의 차이에 절대값을 씌워 평균화 한 것입니다.
MSE는 Mean Squared Error로 실제값과 예측값의 차이를 제곱해 평균화 한 것입니다.
RMSE는 Root Mean Squared Error로 MSE의 값에 루트를 씌운 것입니다.
R2 Square는 결정계수를 의미하며 독립변수가 종속변수를 얼마나 설명하는지에 대한 지표입니다. 즉 우리가 사용한 자료에서 약 91% 정도를 설명하고 있다고 할 수 있습니다.
(각각 지표에 대한 설명은 추후 설명하겠습니다.)
마치며
이번 글에서는 독립변수가 여러개인 데이터를 분석하여 예측하는 다중선형회귀에 대해서 코드와 함께 알아보았습니다. 중간중간 설명이 필요한 부분들에 대해서는 추후 다른 글에서 더 설명해 보도록 하겠습니다.
'Code Example' 카테고리의 다른 글
| Support Vector Machine(SVM)을 활용한 타이타닉 생존자 예측 (0) | 2023.03.16 |
|---|---|
| Random Forest (Titanic 생존자 예측) (0) | 2023.02.09 |
| Decision Tree Code Example(Titanic 생존자 예측) (0) | 2023.02.08 |
| K-Nearest Neighbor Code Example(K-NN - Titanic 생존자 예측) (0) | 2023.01.19 |
| Linear Regression Code Example (0) | 2023.01.11 |




댓글