목차
5. 기울기 소실(Gradient Vanishing) 문제를 해결한 ReLu
안녕하세요. 오션라이트에이아이 백승기연구원입니다.
머리글
이번 글에서는 활성화 함수(Activation Function)과 손실 함수(Loss Function)에 대해서 알아보겠습니다.
활성화 함수란?
활성화 함수란 입력된 신호의 총합을 적절한 출력신호로 변환하는 함수를 뜻합니다.
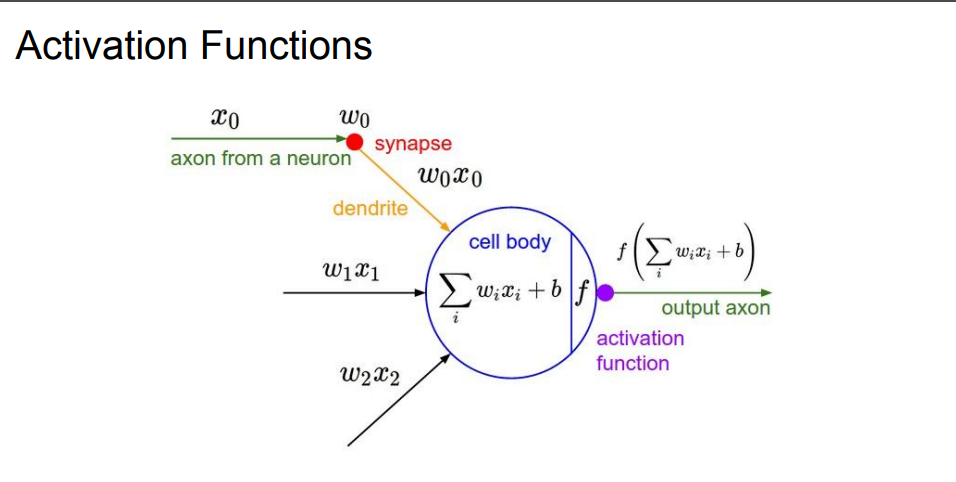
그림 1. 과 같이 입력층으로 들어온 신호를 가중치(Weights)와 편향(Bias)를 계산하고 그것을 적절한 출력으로 만들어주기 위해 사용하는 함수입니다.
활성화 함수의 종류
활성화 함수의 종류에는 Sigmoid, ReLu, tanh 등이 있습니다.
Sigmoid Function
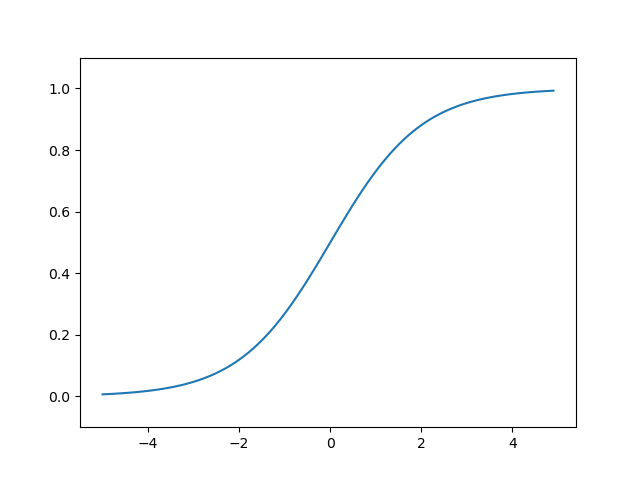
Sigmoid Function은 출력값을 [0,1]사이의 값으로 변환하여 출력해주는 함수입니다.

Sigmoid 함수의 장점
1. 출력값의 범위가 0과 1 사이에 있기 때문에 매끄러운 곡선을 가집니다.
2. 기울기를 측정할 때, 기울기 값이 무한대로 커지는 기울기 폭주(Gradient Exploding)가 발생하지 않습니다.
3. 0과 1 사이의 값을 가지기 때문에 이진분류 문제에서 활용할 수 있습니다.
Sigmoid 함수의 문제점
1. 출력값은 0~1 사이에 존재하기 때문에 입력값이 커지더라도 기울기의 범위가 작아지고 그로인해 기울기 소실(Gradient Vanishing)문제가 발생할 수 있습니다.
기울기 소실(Gradient Vanishing) 문제를 해결한 ReLu
앞에서 살펴보았던 Sigmoid 함수의 문제점인 기울기 소실을 해결한 함수가 ReLu 함수 입니다.
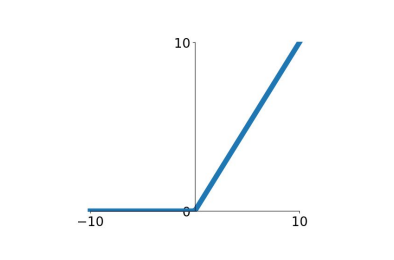
그림 4. 와 같이 ReLu(Rectified Linear Unit)함수는 0이하의 입력값에서는 0만 출력하고 0 이상의 입력값에 대해서는 입력값 그대로 출력합니다.

ReLu 함수의 장점
1. 0 혹은 입력값 이라는 출력값을 가지기 때문에 학습속도가 빠릅니다.
2. ReLu 함수의 편미분 시, 기울기가 1로 일정하므로 가중치 업데이트 속도가 빠릅니다.
ReLu 함수의 문제점
1. 입력값이 음수인 경우에는 기울기가 모두 0이 됩니다.
2. 입력값이 음수일 경우 기울기가 0이기 때문에 가중치 업데이트가 되지 않습니다.
3. 만약 가중치 합이 음수가 되면 ReLu함수는 0을 출력하기때문에 해당 뉴런이 0만을 출력하는 Dead ReLu현상이 생길 수 있습니다.
다중분류에서 사용하는 Softmax Function
위에서 살펴본 Sigmoid 함수는 이진분류에서 사용하였다면 Softmax 함수는 다중분류에서 사용하는 활성화 함수입니다.
Sigmoid 함수에서 0과 1사이의 값에대해 이진분류를 하였다면, Softmax 함수는 n개의 클래스를 분류할 때 n차원의 벡터를 입력받아 각각의 클래스에 속할 확률을 추정합니다.
또한 각각의 출력값의 합이 1이 됩니다.
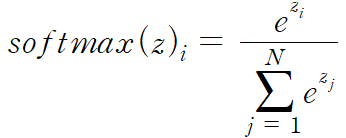
그림 6과 같이 전체 확률을 분모로, 클래스 각각의 확률을 분자로 두어 계산할 수 있습니다.
손실함수
손실함수는 실제 값과 예측한 값의 차이를 구하기 위해 사용하는 함수입니다.
즉, 우리가 예측한 모델의 loss 값이 작을수록 예측을 잘 했다고 할 수 있습니다.
학습을 진행할 때, 정확도는 높이고 loss값을 줄이는 방향으로 진행합니다.
손실함수의 종류
손실함수는 크게 회귀에서 사용하는 함수와 분류에서 사용하는 함수가 있습니다.
회귀에서 사용하는 손실함수
| MSE(Mean Squared Error) | 오차 제곱합의 평균으로 음수값이 나오는것을 방지합니다 |
| RMSE(Root-Mean Squared Error) | MSE에 루트를 씌워서 계산한 값으로 MSE의 값이 커져서 오차를 왜곡하는것을 방지합니다. |
| MAE(Mean Absolute Error) | 오차 절대값 합의 평균으로 MSE와 마찬가지로 음수값이 나오는 것을 방지합니다. |
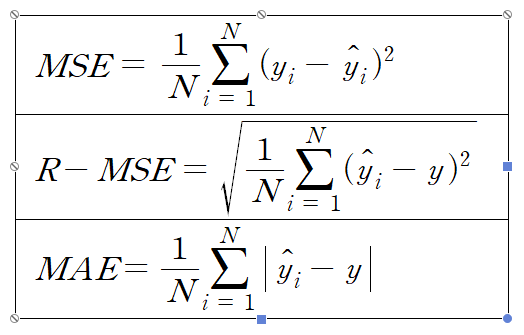
분류에서 사용하는 손실함수
Cross Entropy 손실함수는 실제데이터의 확률분포와 예측한 데이터의 확률분포의 차이를 구하기 위해서 사용합니다.
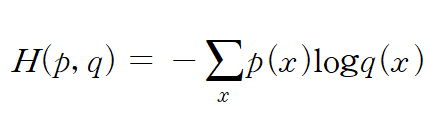
그림 9.를 활용해서 설명하자면, p(x)는 실제 확률값, q(x)는 우리가 예상한 확률값입니다.
만약 p = [0.5, 0.125, 0.125, 0.25], q1 = [0.25, 0.25, 0.25, 0.25],
q2 = [0.5, 0.25, 0.125, 0.125] 이라고 한다면
해당 p와 q1, q2의 Cross Entropy를 구하면 다음과 같습니다.
H(p,q1) = - (0.5log(0.25) + 0.125log(0.25) + 0.125log(0.25) + 0.25log(0.25)) = 약 1.38
H(p,q2) = - (0.5log(0.5) + 0.125log(0.25) + 0.125log(0.125) + 0.25log(0.125)) = 약 1.29
따라서, q2의 예측값이 조금 더 실제 확률분포에 가깝다고 할 수 있습니다.
Cross Entropy는 Binary Cross Entropy와 Categorical Cross Entropy가 있습니다.
| Binary Cross Entropy | True, False 혹은 0 과 1 등의 이진 분류에서 사용할 수 있습니다. |
| Categorical Cross Entropy | 분류해야할 클래스가 3개 이상일 경우에 사용합니다. 각각 클래스에 대한 라벨을 One-Hot Encoding을 통해 변환하여 사용합니다. |
마치며
이번 글에서는 활성화 함수와 손실함수에 대해서 알아보았습니다.
다음 글에서는 역전파 (Back Propagation)에 대해서 알아보도록 하겠습니다.
'바삭한 인공지능' 카테고리의 다른 글
| 바삭한 인공지능(Semantic Segmentation) (0) | 2023.05.09 |
|---|---|
| 바삭한 인공지능(RNN 알고리즘) (0) | 2023.03.02 |
| 바삭한 인공지능(CNN 알고리즘의 종류) (0) | 2023.02.15 |
| 바삭한 인공지능(Convolutional Neural Network) (0) | 2023.01.31 |
| 바삭한 인공지능(딥러닝) (0) | 2023.01.27 |




댓글